打开文本图片集
摘要:Lagrange中值定理在《数学分析》一书中起承上启下作用,它的引入方面可以与图片旋转模式对其几何意义一目了然,通过辅助函数证明其定理。
关键词:Lagrange中值定理;图片旋转;几何意义;辅助函数;证明
一、教材背景分析
在数学分析中,Lagrange中值定理是数学分析中的重要组成部分,为后面Cauchy中值定理具有重大影响作用;同时,在导数中的应用也起着桥梁的作用。
Lagrange中值定理,建立了函数值和导数之间的定量联系,成为我们讨论怎样由导数的已知性质推断函数所具有的性质的有效工具。
二、教学目标
1.知识目标
掌握Lagrange中值定理及对应的几何意义,掌握基本的一些推论。
2.能力目标
首先让同学们了解四大定理(Roll定理,Lagrange中值定理,Cauchy中值定理,泰勒定理),然后通过前期学习的Roll定理,类比学习Lagrange中值定理,培养学生分析、抽象、概括和迁移的学习能力。
3.情感态度与价值观
在教学的过程中,让学生发现教学知识的融会贯通,培养数形结合的思想,以及严密的思维方法,从而亲近数学,爱上数学。
三、教学重难点分析
重点:Lagrange中值定理的引入及其证明。
难点:Lagrange中值定理满足条件的探求,Lagrange中值定理的应用。
四、教学目标
1.通过上节内容学习的Roll中值定理,类比学习和理解Lagrange中值定理,培养数学分析,抽象,概括,迁移的学习能力。
2.通过学习定理,发现数学知识的融会贯通,培养数形结合的思想,以及严密的思维方法。
五、新课讲解
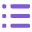
1.Roll定理的回顧与Lagrange中值定理的引入
①在闭区间[a,b]连续;
②在开区间(a,b)可导;
③ .
Roll定理的几何意义已经讲过,如下所示
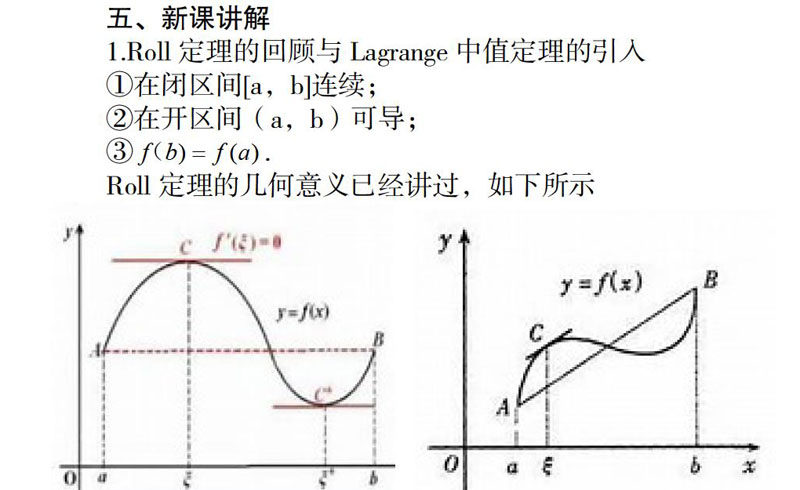
现在我们将这个图形进行旋转,请同学们注意发生的变化大家看看有什么不同。通过旋转得到的图形和原来的图形只是位置发生了改变,但是它的作用也发生了一些变化,通过旋转得到的图形几何意义就是本节课探讨的内容,Lagrange中值定理。
2. Lagrange中值定理
类比前面Roll定理的几何意义猜想出Lagrange中值定理满足的条件
若函数f满足如下条件:
①f在闭区间[a, b]上连续;
②f在开区间(a,b)上可导,
则在(a,b)上至少存在一点ξ,使得
称为Lagrange中值定理.
显然,特别当f(a)=f(b)时,为Roll定理.
3. Lagrange中值定理的证明
具体证明通过借助辅助函数可以证明
证明:作辅助函数
显然,①
②F(x)在[a, b]连续,
③F[x]在(a,b)可导
可得: 命题得证.
4. Lagrange中值定理的几何意义
我们从几何的角度看一个问题,如下:
设连续函数 ,a与b是它定义区间内的两点( ),假定此函数在(a,b)上处处可导,也就是在(a,b)内的函数图象上处处有不垂直与x轴的切线,那么我们从旋转的图容易看到,差商 就是割线AB的斜率,若我们把割线AB作平行于自身的移动,那么至少有一次机会会达到离割线最远的一点 处成为曲线的切线,尔切线的斜率为 ,由于切线与割线是平行的,因此 成立.
补充说明:
它有几种常用的等价形式,可以根据不同问题的特点,在不同场合灵活采用:
参考文献:
[1]数学分析上册/华东师范大学数学系编.—4版.—北京:高等教育出版社,2010.7(2015.5重印).
[2]数学分析中的典型问题与方法/裴礼文.—2版.—北京:高等教育出版社,2006.4(2017.3重印).
[3]微分中值定理的证明及应用中的辅助函数构造/余丽.重庆三峡学院学报.2014.3.
作者简介:向晓凤(1998—),女,汉族,重庆巫溪人,重庆三峡学院在校学生,研究方向:数学教育和计算数学。