打开文本图片集
摘要:曲线曲面拟合技术被广泛应用于医学图像,测试数据,生物防真等众多领域中,分析研究时以数学模型来为工具,采用回归分析或移动最小二乘拟合方法、投影方法和已知数据点约束条件重建曲线曲面方法[1-3]。然而,随着数据量和模型难度的增大,这些方法会产生不良的影响,不能很好的解复杂问题。本文介绍了用matlab实现移动最小二乘法数据拟合的程序流程,并通过算例分析移动最小二乘法的局部近似特性,以及权基函数对近似的影响,从中获得最佳的近似结果。
关键词:MLS法 最小二乘法 数据拟合
中图分类号:TP391.41 文献标识码:A 文章编号:1007-9416(2015)10-0000-00
1 引言
MLS法是对传统加权最小二乘法的进一步推广,克服了最小二乘法的不足,突出了加权函数的紧支性,据此建立的拟合函数,具有局部近似的特点。MLS法的基本理论本文不再赘述详见参考文献[4]。本文针对具体二维和三维算例分析了MLS的局部近似性,为其他研究领域中引入该方法解决复杂问题提供了一种新的思路。
2 算法流程
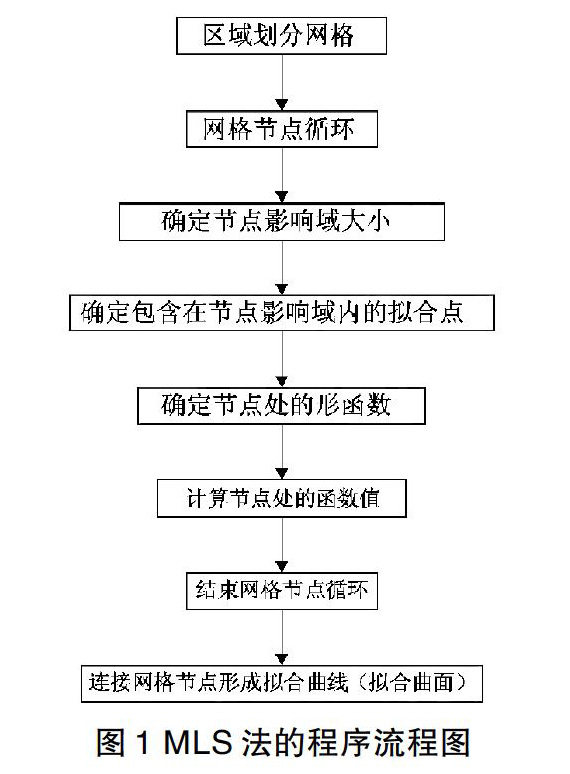
结合移动最小二乘法的特点,给出了基于MATLAB软件编写的MLS法的曲线曲面拟合程序,程序设计流程如图1所示。
3 权函数的影响分析
由图2所示:权函数为恒定常数,样本点的权函数值均为1,在求解过程中系数 不再是自变量x的函数,而是在整个区域内 为常数,可以看出系数 与权函数的选取有关,因此,曲线拟合就退化成最小二乘法的曲线拟合。这样权函数形成的近似为线性拟合。
由图3所示:权函数为紧支常数,只有在中心点 权函数存在非零区域,非零区域尺寸即为节点权函数支持域尺寸,这样在任意一点x的支持域内均有两个节点对其有贡献( ),权函数为1,其他节点的权函数为零,权函数构造的近似就变成了分段线性插值,类似有限元法的函数逼近。由图4所示:权函数为紧支且光滑的函数(三次样条函数),计算点x的支持域内包含的节点数大于基函数的个数( ),为使局部近似误差最小,加权平方和 对 求偏导,最终得到MLS的近似位移,这样的求解过程用于EFG方法中,即使是线性基函数,近似值也是连续光滑的,因为MLS近似继承了权函数的连续光滑性。因此,本部分的分析,选取三次样条函数。
4 曲线拟合
在移动最小二乘法中基函数的选取也有一定的规律,从以上分析,结合表1可以看出:同一个函数采用不同基函数,对计算结果有直接的影响,线性基的基函数的次数越高,逼近效果越好且数值计算的相对误差也越小,二次基函数能够得到良好的拟合效果。
5 曲面拟合
6 结语
移动最小二乘法虽然不具备传统有限元或边界元形函数所具有的插值特征,即不满足 函数的属性,给边界条件处理带来了困难,但是它采用了较低的基函数通过选取适当的权函数,获得具有较高连续性和相容性的形函数,数值精度较高,数据简单等特点,是其他数值近似方法无法比拟的,对以后的数值近似的研究具有重要的参考价值。
参考文献
[1] 王能超.数值分析简明教程[M].北京:高等教育出版社,2003.
[2] 常青,余湘娟.软土次固结变形特性的试验研究[J].南水北调与水利科技,2008(1):148- 150.
[3] 张荣.利用VB实现水泵性能曲线的自动绘制[J].水利科技与经济,2006(1):62- 64.
[4] 程玉民.移动最小二乘法研究进展与述评[J].计算机辅助工程,2009(2):5-11.
收稿日期:2015-09-21
作者简介:蒋博(1987—),男,河南洛阳人,硕士,助理工程师,研究方向:结构设计理论。